Objective resolution refers to the ability of the objective to distinguish two closely adjacent features, and is theoretically commonly expressed as the minimum distance between two distinguishable point sources. The image of a point source is not a bright spot due to diffraction, but an extended light intensity profile. This contour, called the Airy spot, consists of a central bright spot and a series of concentric rings of alternating light and dark with significantly reduced intensity. Thus, the image of two point sources is two overlapping airy spots, and the resolution of the objective depends on the minimum resolvable distance between the two.
Although there is no basic standard for determining whether two airy spots are distinguishable, there are still some criteria for reference in practical applications. In microscope imaging, two commonly used criteria are Rayleigh criterion and Abbe criterion. The third is the Carrol Mason Sparrow criterion, which is commonly used in astronomy.
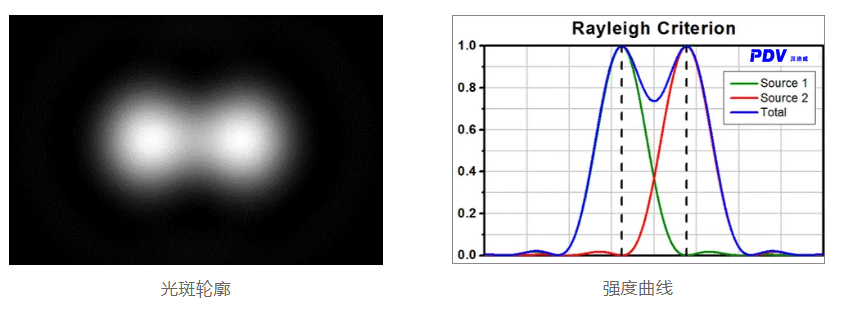
Rayleigh criterion
The Rayleigh criterion states that when the first intensity minimum of one airy spot coincides with the maximum of the other Airy spot, the two airy spots are distinguishable. With the central maximum as the center of the circle, the first intensity minimum is located on a ring with a radius of 1.22λf/D, where λ is the wavelength of light, f is the focal length of the objective, and D is the diameter of the entry pupil.
If expressed in numerical aperture (NA), the Rayleigh resolution is:
r(R) = 1.22λf/D = 0.61λ/NA
The lower left figure shows two ideal Airy spots with spacing equal to Rayleigh resolution (assuming the illumination source is incoherent), while the lower right figure shows the corresponding light intensity curve. As can be seen by the two vertical dashed lines, the maximum value of each airy spot coincides with the minimum value of the adjacent airy spot. In addition, there is a local minimum between the two maxima, which appears clearly in the gray area between the two white spots.
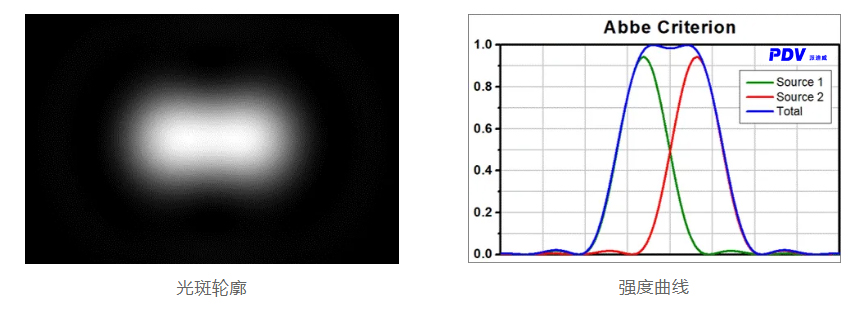
Abbe criterion
In Abbe's theory, imaging is a double diffraction process. In this theoretical framework, in order to distinguish two features separated by d, it is required that both zero-order and first-order diffraction can pass through the objective. Because the Angle of the primary diffraction is sinθ₁ = λ/d, the minimum distance between the two features (objective resolution) is d = λ/(n· Sinα), where α is the half Angle of the aperture of the objective and n is the refractive index of the imaging medium.
The above result is twice the actual resolution limit because it assumes that both first-order diffraction pass through the objective, but in reality only one first-order diffraction and zero order diffraction are required. Dividing the above result by 2 and substituting it into the expression NA yields the famous Abbe resolution:
r(A) = 0.5λ/NA
The lower left image shows two ideal Airy spots with a distance equal to Abbe resolution, while the lower right image is the corresponding light intensity curve. The minimum at the origin is much more difficult to distinguish than the Rayleigh resolution, because it is only about 2% below the two intensity maxima.
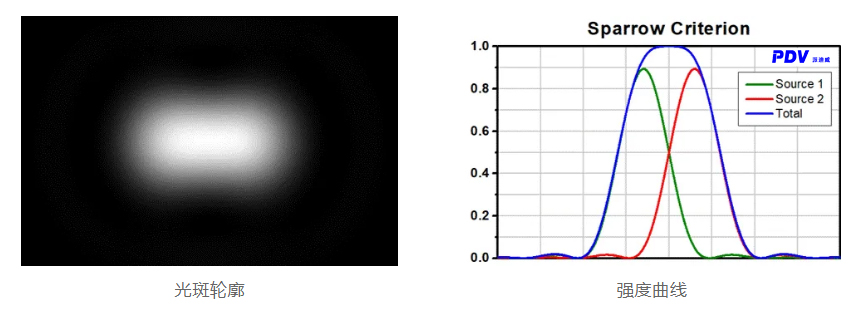
Sparrow's criterion
For Rayleigh and Abbe resolutions, the resultant intensity profile of the two point sources has a minimum, located at the origin halfway between the two maxima. In a sense, this is the reason why the two point sources can be distinguished. If the spacing is further reduced until it is less than the Abbe resolution limit, the two separate maxima will merge into a single central maximum and become indistinguishable. Thus, the Sparrow resolution criterion states that when the center transitions from a minimum to a maximum, the spacing between the two point sources reaches the resolvable limit.
At Sparrow resolution limit, the center of the resultant intensity profile is flat, indicating that the derivative of strength with respect to position is zero at the origin. But this does not tell whether the strength at the origin is a maximum or a minimum. Since the Sparrow resolution limit occurs when the origin strength transitions from a local minimum to a maximum, the sign of the second derivative must change from positive to negative.
Thus, Sparrow's criterion is based on the second derivative. When the second derivative at the origin is zero, the resolution reaches its limit. Applying this condition to the resultant intensity profile of two airy spots yields Sparrow resolution:
r(S) = 0.47λ/NA
The lower left image shows two Airy spots with spacing equal to Sparrow's resolution, while the lower right image shows the corresponding light intensity curve with no intensity depression at the origin.